复赛选题｜海泰方圆为全国密码技术竞赛设计了一种大分组算法

近日，海泰方圆荣幸地收到了来自中国密码学会的感谢信。信中表示公司精心设计的题目《一种组合式大分组分组密码算法的软件实现及应用》已入选2024年第九届全国密码技术竞赛复赛题库。同时，该题目被武汉大学选用并获得了二等奖的佳绩。这一喜讯不仅是对海泰方圆在密码技术领域深厚底蕴与卓越专业能力的有力证明，更是密码竞赛组委会诸位专家对公司在密码技术研究与创新探索道路上不懈努力的充分认可与高度赞誉。

本文围绕该入选题目展开深入讨论，分析量子计算对密码安全的潜在威胁，探讨对称密钥密码方面可能的应对策略与未来发展方向。我们诚挚邀请各位专家学者、行业同仁以及对此领域感兴趣的读者积极参与讨论，共同为推动密码技术的创新发展与国家信息安全保障贡献力量。

电话：17600993730（微信同号）

1.    引言

量子计算在攻击对称钥密码算法方面的能力是密钥减半关系已被学术界认可。这样，2²⁵⁶的密钥穷尽量，在量子计算面前有可能相当于2¹²⁸的计算量，被公认为是暂时安全的。而密钥长度128比特，即密钥穷尽量为2¹²⁸，通常是传统计算机无法有效穷尽的，可是在量子计算面前，这相当于2⁶⁴的量子比特密钥穷尽量，是相当脆弱的，是可以攻克的。

作为国家商用密码标准的分组密码SM4算法能支持的密钥长度只有128比特。没有预先考虑128比特密钥长度不够用或不够强的问题。量子计算导致的安全威胁日渐临近，必须防患于未然。所以，有必要改造和设计一种能够支持较长密钥的分组算法，支持长度为128、256、384和512比特的密钥，可以用于类似密钥封装这样的高度敏感数据的加密传输。

在国家推出256比特或更长密钥长度的分组密码标准算法之前，需要有一个过渡时期的替代品，应对偶尔需要的高度敏感数据的高安全强度加密问题，尤其是应对即将来临的量子计算攻击。

另一方面，中国密码学会向海泰方圆公司征集2024 第九届全国密码技术竞赛的复赛题目，为此，海泰方圆设计了一种512比特分组、可支持512比特密钥的分组密码方案。将该方案的密码软件优化实现和场景应用作为复赛题目，期望参赛队伍依此展示和发挥密码技术能力。也期望该方案激发密码学术界的评论和探索。

2.    基于SM4和SM3的大分组分组密码方案

为了提高国密分组密码算法的安全强度，为了能抵御量子计算攻击，海泰方圆公司设计了一种基于国密算法SM4和SM3的组合式大分组密码算法，可以支持包括512比特的多种密钥长度。可以用于高度敏感数据的安全保护。

该大分组分组密码算法方案的分组长度为512比特，密钥长度有128、256、384、512比特。基础组件是SM4和SM3算法，采用类Feistel结构的SP结构，迭代4轮，见图1 。

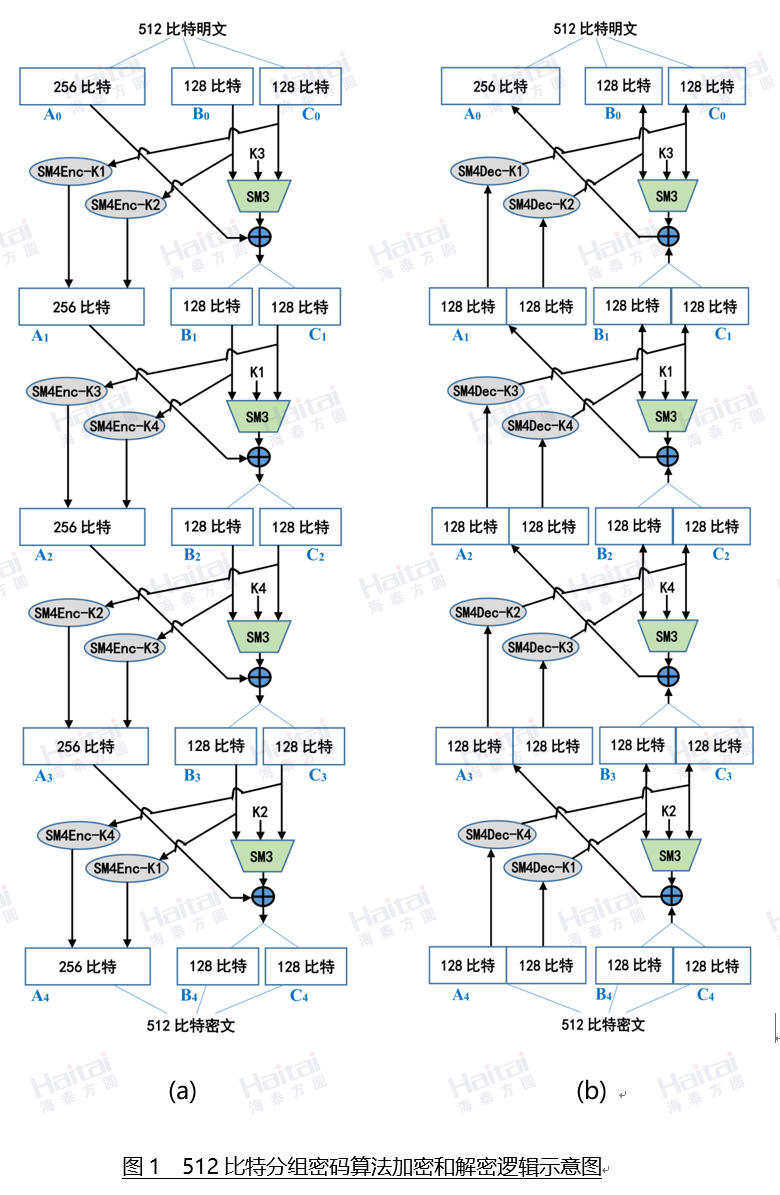
图中的“SM3”表示用SM3算法对输入的384比特数值（3个128比特串接），计算产生 256比特hash值。

图1(a)中SM4Enc-Ki表示以Ki为密钥，将128比特数据加密，i=1,2,3,4。通常将K1、K2、K3和K4称为轮密钥。加密时，将输入的512比特数据分为三部分，左256比特记作为A_i-1，右256比特的左128比特记作B_i-1，最右边128比特记作C_i-1，即512比特输入值被表示为A_i-1| B_i-1| C_i-1。输出的512比特值记为A_i| B_i| C_i，i=1,2,3,4。例如当i=1时有：

A₁ =SM4Enc_K1(C₀) | SM4Enc_K2(B₀).

B₁| C₁ = SM3(B₀ | K3 | C₀ ) ⊕ A₀.

不同轮的计算表达式相同，只是使用的轮密钥不同。

图1(b)是解密逻辑示意图，图中SM4Dec-Ki表示以Ki为密钥，将128比特数据解密，i=1,2,3,4。解密时，将512比特密文组分割为A₄|B₄|C₄，其中A₄为256比特，B₄为128比特，C₄为128比特。以A₄的左128比特为输入，以K4为密钥，用SM4算法解密，得到C₃。以A₄的右128比特为输入，以K1为密钥，用SM4算法解密，得到B₃。将B₄和C₄联接为256比特B₄|C₄。将B₃、K2和C₃联接为384比特数据串B₃|K2|C₃，用SM3算法对B₃|K2|C₃计算hash值，得到256比特乱数，用该乱数与B₄|C₄异或，得到A₃。这样就有了逆推一轮的512比特A₃|B₃|C₃。如此，可逐轮地逆推到A₀、B₀和C₀。

当使用128比特密钥时，全部密钥为K1，K2=K3=K4=K1。

当使用256比特密钥时，左128比特为K1，右128比特为K2，K3=K1，K4=K2。

当使用384比特密钥时，左128比特为K1，中128比特为K2，右128比特为K3，K4=K1⊕K2⊕K3。

当使用512比特密钥时，按4个128比特，密钥被分割为K1、K2、K3和K4。

由于SM4和SM3算法具有公认的密码学安全性，算法以它们为逻辑函数组件，其安全性会远比SM4和SM3算法强。传统的差分分析和线性分析难以产生明显的分析效果。如果攻击者有能力破译SM4算法，则他有能力破译该大分组算法的一轮。攻击两轮的难度会大幅度上升，攻击4轮的难度是难上加难。该设计方案中有两个问题需要深入研讨，一是当使用256、384或512比特密钥时，算法能否相应地提供不少于256、384或512比特密钥穷尽量的安全强度。二是当使用256或512比特密钥时，算法能否具有不少于128或256个量子比特的抗量子攻击强度。

3.    结束语

由于量子计算研究方面不断取得进展，抗量子密码的研究和应用迫在眉睫，抗量子密码新理论和成果应用及量子迁移，将是一段相当长的逐渐演变过程。在成熟的对称钥密码抗量子方案出台之前，不妨用图1中的算法方案救急一些重要数据的安全防护。尽管不能给出精准的算法抗量子计算攻击和抗传统密码分析的底数，但是，由于算法中引用了成熟的SM4和SM3算法，有理由相信这类逻辑组件在非线性变换效果和抗相关分析方面保持原有的性能。