前沿技术|保留格式加密的双扰工作模式
发布时间: 2022-10-30 09:13引言
为防止一些敏感信息被人偷窥,信息加密是一种较好的应对措施。但有些情形并不需要对大量明文进行加密,比如,有一些表格,每张表格上只有手机号、身份证号和电子邮箱地址等较为敏感,其它内容无需加密。如果将这些数字串或字符串用AES或者SM4等分组密码算法加密,需要按128比特(16字节)数据组作分组处理,产生的密文是16个字节,有些字节是不方便打印的。如果将16字节密文转换成为十进制数字,一般会变为一个39位数,不仅表格内写不下,操作起来也不方便。为解决这类问题,一些保留格式加密(Format Preserving Encryption,FPE)算法方案被提出并开始走向应用。2011年美国NIST曾经推荐将源自FFX方案[2]的保留格式加密算法FF1和FF3确立为AES标准工作模式。
保留格式加密算法能够将N个数字加密成N个数字,将一串字母加密成同样长度的一串字母,即加密后它能使密文保持明文的长度和数据类型。近年来出现了很多种保留格式算法方案,但是多数方案都难以被推广应用。困扰这些方案的核心问题是实用性和安全性。如果不允许明文组(和密文组)空间较小则不实用。如果允许明文组(和密文组)空间很小,可能会有安全隐患。为此,我们提出一种专门的保留格式算法工作模式,较好地规避因明密文空间较小可能引发的安全问题。期望它也许能够为一些存在安全隐患的保留格式加密方案装上一层防护盔甲。
另外,近几年出现了一些以功率消耗少、内存占用少为特点的轻量级分组密码算法。有些轻量级分组密码算法的分组长度只有32比特,在较长的密文数据段中容易存在密文组重复。如果是ECB(电子密本)模式加密,密文组重复意味着出现了明文组重复。这意味着分组较小时报文明文格式特征易于外露。本文给出的双扰工作模式能够弥补分组密码算法因明文组(密文组)空间较小引发的某些安全缺陷。
1. 保留格式算法的一种双扰工作模式
绝大多数保留格式加密算法都属于分组密码算法。说起分组密码的工作模式,默认的模式自然是ECB。可是,像DES、AES等密码算法还可以有OFB(输出反馈)、CFB(密文反馈)、CTR(计数器)等工作模式。当AES(或DES)算法以OFB、CFB或CTR模式工作时,通常被称为分组密码算法以序列方式工作,本质上这已经是序列密码,不再拥有分组密码的代替作业特征。对于一般的保留格式加密算法,默认的工作模式也是ECB,即一组码符被替换成另一组码符,解密时把它替换回来。如果要对长段码符的多个分组进行保留格式加密,除了ECB模式,能否采用类似OFB、CFB或CTR等序列模式呢?因为保留格式加密很可能要面对明密文空间较小的情形,以序列密码方式工作时会因为乱数序列周期较小而被破译。
正是由于保留格式加密方案允许明密文空间较小,当攻击者获得了很多个明密对以后,有可能因为密文组碰撞导致更多报文的明文泄露,甚至成就攻击者有条件尝试一些针对密钥的已知明文攻击。为此,我们提出一种“双扰工作模式”。其基本思想是对明文组和密文组加扰。明文组(密文组)由若干个码构成,每个码可看作是一个m进制数,加扰是码与码对应相加,约定其为按位模m加(码间没有进位),用符号“◎”表示。其逆变换为按位模m减,用符号“Θ”表示。例如,字符集大小m=10,每组码数N=4,分组码0567与7538的模10加为0567◎7578=7035,0567与7538的模10减为0567Θ7578=3099。
设明文字符集大小为m,分组长度为N个码符。用FPEnc(P,K)表示用密钥K对明文组P作ECB模式保留格式加密。如果使用IV(初始向量)且IV与明文组类型不同,则需要按某规则将IV转化为N位m进制数,使IV与明文组同类型。若不使用IV,则默认IV=0。双扰工作模式的加密方法如下:
1) 以N个码为一组,将明文段分为t个组P1,P2,P3,……,Pt。
2) 用密钥K将IV加密(如果不使用IV则将“0” 加密),得S0=FPEnc(IV,K),称S0为秘密IV。计算S1=FPEnc(0◎S0,K)=FPEnc(S0,K)。对i=2,3,……t,计算Si=FPEnc((Si-1◎Si-2),K)。得到扰序列S0、S1、S2、……St。
3) 加密各个明文组。对i=1,2,3,……t,做如下三小步:
A. 将明文组Pi与扰码Si-1按位模m加(明文加扰),得P=Pi◎Si-1。
B. 将P加密,即得到C=FPEnc(P,K)。
C. 将C与Si按位模m加(密文加扰),即
Ci=C◎Si。Ci为第i个密文组。
参见图1。
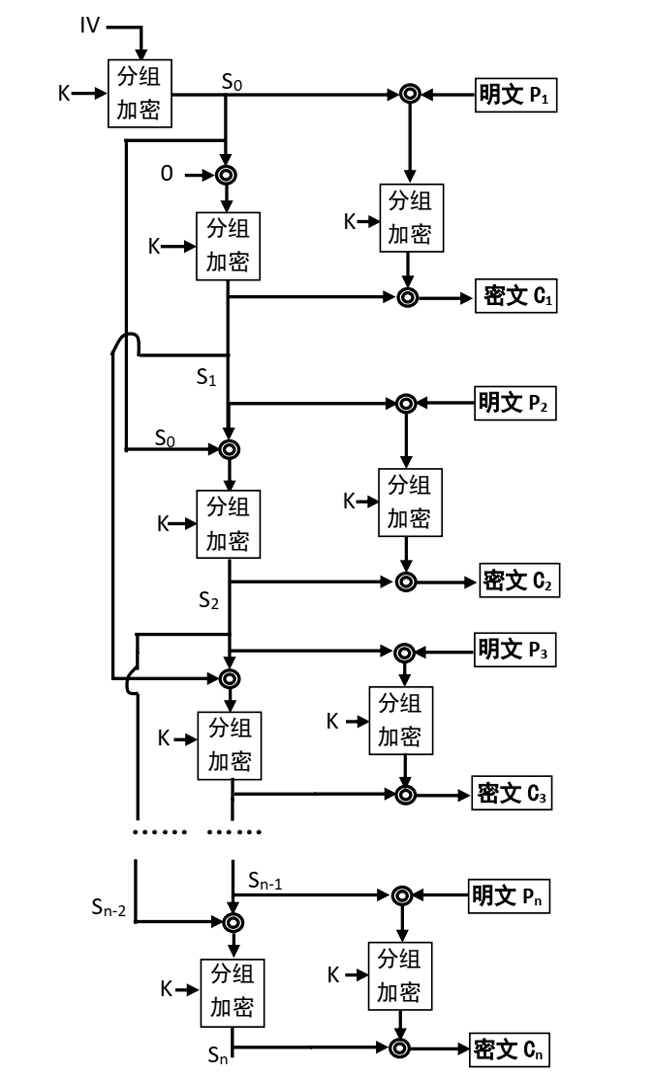
图1 双扰工作模式分组加密流程示意图
双扰工作模式的解密方法与加解方法相似,需要加解密双方约定是否使用IV。解密时步骤3)中的加密运算相应地变为解密运算,按位模m加相应地变为按位模m减,参见图2。即步骤3)相应地变为对i=1,2,3,……t,做:
A. 将密文组Ci与扰码Si按位模m减(密文解扰),得C=CiΘSi。
B. 将C解密,即计算P=FPDec(C,K)。
C. 将P与Si-1按位模m减(明文解扰),即解得明文组Pi=PΘSi-1。
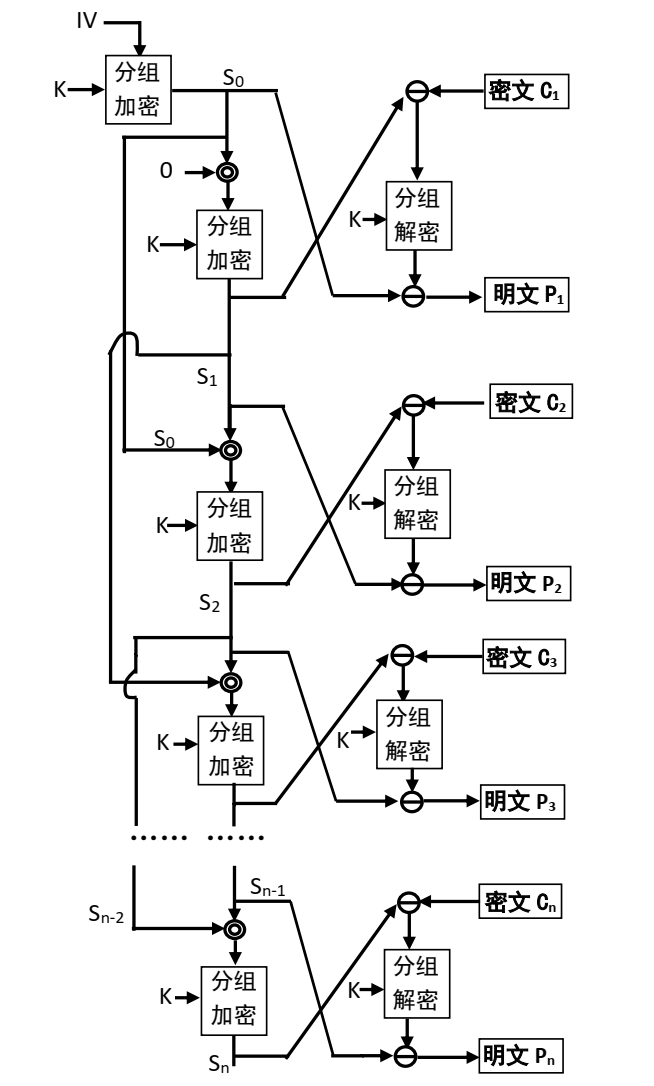
图2 双扰工作模式解密流程示意图
上述三小步可用式子描述为:
Pi=FPDec((CiΘSi),K)ΘSi-1。
IV的作用在于产生扰码序列初值S0。对攻击者来说,IV是可见的,但S0是不可预测的。不同的IV产生不同的S0,导致产生不同的扰码序列。
2. 对双扰工作模式的性能分析
海泰方圆设计的保留格式加密算法的双扰工作模式实际是将ECB模式与序列加密模式相互混合,可以直观地理解为每个数据组的加密过程分为三步:第一步,用一组扰码对输入的明文组实施加扰。第二步,对加了扰的明文组作多轮迭代式分组加密。第三步,用另一组扰码对分组加密后的输出密文进行加扰。对于实用的现代分组密码算法,唯密文攻击几乎没有成功希望,所以,较为现实的攻击方向当属已知明文攻击和选择明文(密文)攻击。为了能够形成攻击所需要的数据条件,攻击者必须设法搜索和猜设一定数量的明密对。
在通常的ECB或CBC(密文分组链接)工作模式情形,当攻击者截获了某用户的长段密文后,通过研究密文产生场景、收集与该用户相关的相近长度明文数据、关注密文解译方公开流露出的等长明文段落等,将某些明文段与密文段形成明密对应,进而猜设到一些明密对。甚至有可能找到密文组重复,暴露明文结构特征,为猜设明文提供重要佐证。之后,可以开展一些已知明文攻击或选择明文攻击类研究课题。当明文组空间较小时,如果密文数据量较大,这类攻击有可能产生实质效果。
在CBC工作模式情形,假设用户加密明文段P=(p0,p1,p2,…,pn)产生了密文C=(c0,c1,c2,…,cn),而且用户在不变更密钥情况下又加密明文段Q=(q0,q1, q2,…,qm)产生了密文D=(d0,d1,d2,…,dm)。如果攻击者在C和D这两份密文之间找到了相同的密文组,比如有ci=dk,1≤i≤n,1≤k≤m。那么,依据分组迭代时相同的密文输出必定有相同的明文输入,攻击者可以推出ci-1⊕pi=dk-1⊕qk,得到ci-1⊙dk-1= pi⊙qk,这里“⊕”表示数据组异或,“⊙”表示逻辑同。进而有pi⊕qk=ci-1⊕dk-1。由于ci-1和dk-1在密文中可见,ci-1⊕dk-1是已知的。因此,通过找到和研究相同密文组,攻击者可以发现两明文组间的差值,这将有助于猜设明文。同理,若在一份较长密文内找到了相同密文组,比如有ci=ck,可以获知明文组pi与pk间的差值。所以,若能在密文数据中找到相同的密文组,CBC模式是有安全缺陷的,而双扰工作模式不存在此类安全隐患。
在CTR或OFB模式情况,如果用户不慎重复使用了IV,会导致信息泄露。而在双扰工作模式情形,重用IV意味着分组序号相同的两个数据组,加在明文上的扰码相同、加在密文上的扰码也相同,具体扰码是什么不可预测。其攻击难度大于ECB模式只有两个明密对时,求取密钥或者预测其它明密对。即使同一个IV重复使用 n次,双扰工作模式的安全强度也会优于已知n个明密对情形的已知明文攻击。
双扰工作模式的中心思想是通过多次加密IV产生秘密扰码序列,扰乱分组迭代的输入和输出。如果用户采用了本文给出的双扰工作模式,即使攻击者获得了某密文段落的明文,仍然得不到明密对,因为攻击者不能准确地猜设用于明文组和密文组的扰码。当明文组序号不相同时,即使出现相同的密文组也无助于猜设明文信息。
拥有若干明密对构成的适度数据条件,是密码分析和破译的基本素材,也是破译成功的必备基础。双扰工作模式遏制了攻击者获取有效数据的能力,使攻击者不能具备开展密码分析研究的数据条件。破坏了攻击者的攻击能力,某个层面上等同于该工作模式增强了算法的安全强度。
由于双扰工作模式每加密一个明文组近似等于做两次ECB加密和两次按位模m加,在效率方面它只相当于通常CBC或CTR模式的近似二分之一。大多数情形,这不会影响实际应用。另外,由于扰码的产生与明密文无关,致使扰码序列可以预计算或并行计算,从而可以使双扰工作模式的运算时间在可并行环境下逼近CBC模式。
结 论
算法的工作模式也是算法安全性的一个组成部分。好的工作模式可以弥补算法设计上的某些不足,它可以为算法安全性加分,但也可能为算法工作效率减分。安全与效率通常是相互制约的两个方面。对于保留格式加密算法,面对的场景可能是明文组空间较小,需要加密的数据量不大。所以,实际应用中用户对效率的要求不高,安全性更为重要,这将使得双扰工作模式拥有较好的应用前景。其实,海泰方圆设计出的双扰工作模式实质上是分组密码算法的一种通用工作模式,它并不局限于保留格式加密中的应用,仅仅是用于保留格式加密算法时,因为数据分组可能较小,安全性方面的优点较为突出。















